Założenia
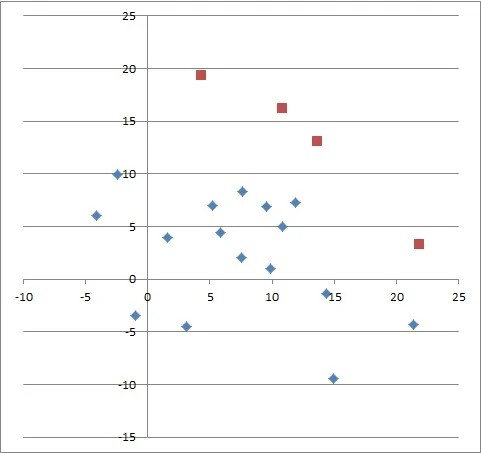
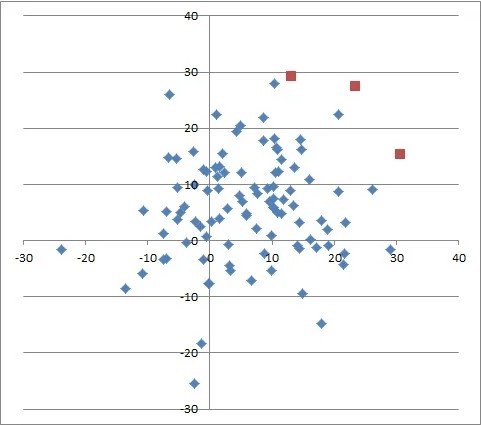
Przyjmijmy, że mamy zbiór punktów w przestrzeni n-wymiarowej, przy czym współrzędne pojedynczego punktu są reprezentowane w postaci wektora liczb rzeczywistych o długości n. Mówimy, że punkt A dominuje nad punktem B, jeżeli dla każdej współrzędnej A(i) odpowiadająca jej współrzędna B(i) jest mniejsza lub równa, oraz istnieje co najmniej jedna taka współrzędna j dla której A(j)>B(j). Można też wtedy powiedzieć, że B jest zdominowane przez A. Jeżeli natomiast dla pary punktów taki warunek nie jest spełniony, tj. ani A nie dominuje nad B, ani B nad A, wtedy uważamy punkty A i B za nieporównywalne względem siebie.
W zbiorze punktów punkt niezdominowany to taki, który może tylko dominować lub być nieporównywalnym z wszystkimi pozostałymi punktami.
Zadanie #1
Wygeneruj zbiór 100 losowych punktów w przestrzeni n-wymiarowej, po czym znajdź w nim zbiór punktów niezdominowanych. Algorytm znajdowania punktów niezdominowanych polega na porównaniu każdego punktu ze wszystkimi pozostałymi (nie dokonujemy porównania punktu z samym sobą). Jeżeli dla aktualnie sprawdzanego punktu z żadnego porównania nie wyniknie, że jest zdominowany, to znaczy, że jest niezdominowany. Kopię znalezionego punktu niezdominowanego należy zapisać w kontenerze pomocniczym. Na koniec sprawdzania kontener pomocniczy zawiera wyłącznie punkty niezdominowane.
Algorytm można zrealizować z pomocą dwóch kontenerów zawierających zestawy tych samych 100 punktów oraz kontenera pomocniczego, który początkowo jest pusty. Punkty z pierwszego kontenera są punktami sprawdzanymi, a punkty z drugiego – punktami z którymi dokonywane jest sprawdzenie. Do kontenera pomocniczego trafiają kopie tych punktów z kontenera pierwszego, które okazały się niezdominowane. Realizacja czynności odbywa się za pomocą dwóch pętli for – zewnętrznej (punkty z pierwszego kontenera) i wewnętrznej (punkty z drugiego kontenera).
Po zaimplementowaniu algorytmu spróbuj zaimplementować go ponownie, ale tym razem bez używania pętli for, while, repeat, natomiast stosując algorytmy STL oraz własne lub biblioteczne obiekty funkcyjne. Sprawdź, czy uzyskałeś ten sam wynik.
Zadanie #2
Wygeneruj zbiór 100 punktów losowo rozłożonych na okręgu (w przestrzeni 2-wymiarowej) o promieniu 1 (zobacz Zadania przed lab. 6: zadanie #2), po czym znajdź w nim zbiór punktów niezdominowanych. W kontenerze uporządkuj rosnąco niezdominowane punkty pod względem ich pierwszej współrzędnej. Wykorzystując algorytm adjacent_difference (slajdy 121 i 122, wykład 9) policz odległości euklidesowe miedzy sąsiednimi punktami (tj. między punktami 1 i 2, 2 i 3, 3 i 4, itd.). Uwaga: w obiekcie funkcyjnym służącym do obliczenia odległości euklidesowej miedzy dwoma punktami skorzystaj z algorytmu inner_product, tak jak to jest pokazane na slajdzie 121 wykładu 9. Policzone odległości zapisz do pomocniczego kontenera, a na koniec policz średnią odległość między punktami oraz wariancję tej odległości.
Przy pisaniu kodu programu unikaj pętli for, while, repeat, a zamiast nich stosuj algorytmy STL oraz własne lub biblioteczne obiekty funkcyjne.
Wskazówka: kod zawierający przykładowy fragment rozwiązania zadania 2 – wykorzystanie algorytmu inner_product do policzenia odległości euklidesowych miedzy sąsiednimi punktami: ZTP_Zad2przedLab7.cpp
Hint:
Zadanie dotyczące znajdowania zbioru punktów niezdominowanych może pojawić się na lab.7. Na zajęciach można będzie wykorzystać fragmenty własnego kodu opracowanego w domu.

